2019

2019 Paper 2 Question 16

nstmathsupervisorLeave a comment

(a)

I = \int\int_S (z+y^3) dS = I_1 + I_2 + I_3

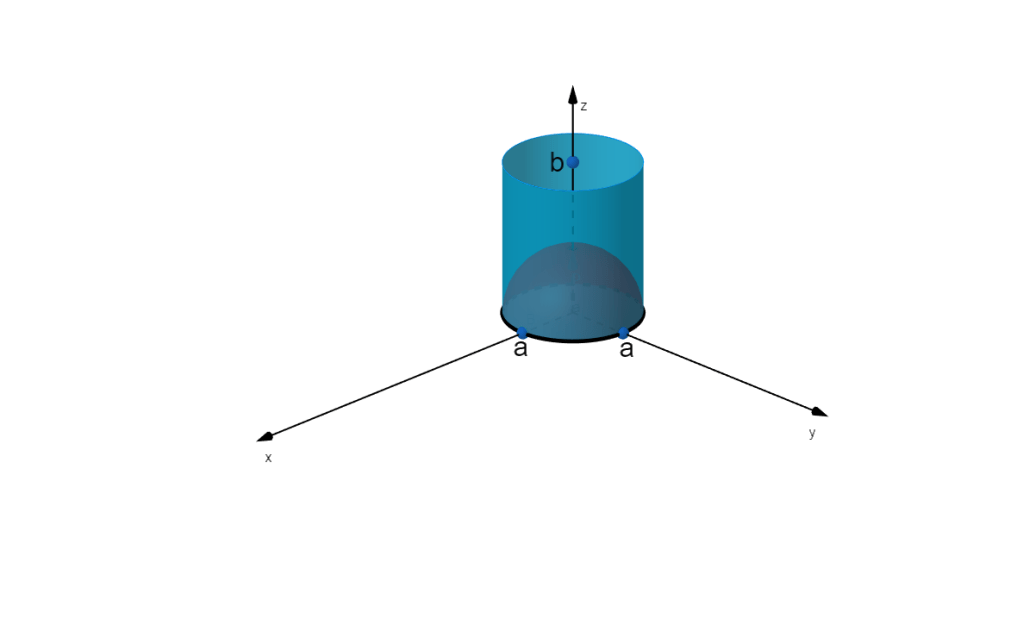
where I_1 is the integral over the upper circular surface, S_1, at z=b, I_2 is the integral over the cylindrical surface, S_2, and I_3 is the integral over the lower hemi-spherical surface, S_3.

Each integral will be computed by appropriately parameterising the surface.

For I_1

z=b \quad dS=dx\,dy

I_1 = \int\int_{S_1} (b+y^3)dx\,dy

Change to plane polar coordinates

\begin{aligned} I_1 &= \int\limits_{\theta=-\pi}^{\pi}\int\limits_{r=0}^{a} (b+r^3 \sin^3\theta) r dr d\theta \\ &=b\pi a^2+\int\limits_{\theta=-\pi}^{\pi}\sin^3\theta d\theta \int\limits_{r=0}^{a} r^4 dr \end{aligned}

The angular integral is zero (integrating an odd function over a symmetric range). Hence

I_1 = \pi a^2 b.

For I_2, using cylindrical polar coordinates

y=a \sin\theta, \, z=z

\begin{aligned} I_2 &= \int\int_{S_2} (z+y^3)dS \\ &= \int\limits_{\theta=-\pi}^{\pi} \int\limits_{z=0}^{b} (z+a^3 \sin^3\theta) a d\theta dz\\ &= a\int\limits_{\theta=-\pi}^{\pi} d\theta \int\limits_{z=0}^{b} z dz+a^4 \int\limits_{\theta=-\pi}^{\pi}\sin^3\theta d\theta \int\limits_{z=0}^{b} dz \end{aligned}

As above, the \sin^3\theta integral is zero, hence

I_2 = \pi a\ b^2.

For I_3, parameterise S_3 with spherical polar coordinates

\begin{aligned} z &= a \cos\theta \\ y &=a \sin\theta \cos\phi \\ dS &= a^2 \sin\theta d\theta d\phi \end{aligned}

So

\begin{aligned} I_3 &= \int\limits_{\theta=0}^{\pi/2}\int\limits_{\phi=-\pi}^{\pi}(a\cos\theta+a^3\sin^3\theta\sin\phi) a^2 \sin\theta d\theta d\phi \\ &= a^3\int\limits_{\theta=0}^{\pi/2}\int\limits_{\phi=-\pi}^{\pi} \sin\theta \cos\theta d\theta d\phi + a^5 \int\limits_{\theta=0}^{\pi/2}\int\limits_{\phi=-\pi}^{\pi} \sin^4\theta \sin\phi d\theta d\phi \\ &= 2\pi a^3 \left[ \frac{1}{2}\sin^2\theta \right]_{\theta=0}^{\pi/2} + a^5\int\limits_{\theta=0}^{\pi/2}\sin^4\theta d\theta \int\limits_{\phi=-\pi}^{\pi}\sin\phi d\phi \\ &= \pi a^3 + 0 \end{aligned}

because the integral over \phi equals zero.

Finally we arrive at

\begin{aligned} I &= I_1 + I_2 + I_3 \\ &= \pi a^2 b + \pi a\ b^2 + \pi a^3 \\ &= \pi a (b^2+ab+a^2) \end{aligned}